Basics 2

Booleani

Slide adattate da softpython

Clicca qui per la versione stampabile

Premi esc per l'overview generale

1. Introduzione 1/1

Cosa sono i booleani?

  • Usati nell'algebra booleana
  • Il loro tipo è bool
  • I valori di verità sono True o False
  • Riesci a creare una variabile che venga valutata come falsa?

1. Introduzione 1-2

L'algebra booleana

a b a and b
True True True
True False False
False True False
False False False
a b a or b
True True True
True False True
False True True
False False False
a not a
True False
False True

1. Introduzione 2-1

Il tuo turno!

  • Prova ad indovinare il risultato delle espressioni sulla destra
  • Inserisci la tua risposta nella variabile risp
  • Infine esegui il codice e verifica il tuo punteggio

Altri esercizi

1. Introduzione 2-2

1. Introduzione 2-3

Domande con variabili

  • Qui devi assegnare i corretti valori a x e/o y per fare in modo che l'espressione ritorni True
  • Nota che ci possono essere più combinazioni che producono True!
  • Riesci a trovarle tutte?

1. Introduzione 2-4

Come prima!

1. Introduzione 2-5

Al contrario!

  • Per quali valori di x,y e/o z le espressioni ritornano False?

2. De Morgan 1

De Morgan

Formula Equivalente a
x or y not(not x and not y)
x and y not(not x or not y)

Queste leggi tornano spesso molto utili, cerca di ricordarle

2. De Morgan 2

Il tuo turno!

  • Prova a riscrivere le espressioni che ti verranno proposte in una maniera equivalente usando le leggi di De Morgan
  • Prova a semplificare il risultato ove possibile
  • Infine esegui il codice e verifica il tuo punteggio
  • Alla destra trovi un esempio, vai avanti per gli altri esercizi
Formula Equivalente a
x or y not(not x and not y)
x and y not(not x or not y)

3. Conversioni 1

Conversioni

  • Abbiamo visto che i possibili valori per booleani sono True e False
  • Ma booleani possono essere anche convertiti ad interi, e vice versa!
  • Come sono gestiti i valori di verità quando si effettuano queste conversioni? Prova a scoprirlo
  • Ogni intero è valutato a True, eccetto per 0
  • I valori di verità True e False si comportano rispettivamente come gli interi 1 e 0
  • bool(1) -> True
  • bool(0) -> False
  • bool(72) -> True
  • bool(-5) -> True
  • int(True) -> 1
  • int(False) -> 0

3. Conversioni 2

Il tuo turno!

  • Prova ad indovinare il risultato delle espressioni sulla destra
  • Inserisci la tua risposta nella variabile risp
  • Infine esegui il codice e verifica il tuo punteggio

4. Ordine di Valutazione 1

Ordine di valutazione

  • Se durante la valutazione di un’espressione booleana Python scopre che il risultato possibile può essere solo uno, allora evita di calcolare le espressioni seguenti.

4. Ordine di Valutazione 2

Ordine di valutazione

  • Se invece la valutazione continua, il risultato sarà la valutazione dell’ultima espressione
  • True and 5 -> 5
  • 5 and True -> True

4. Ordine di Valutazione 3

Ordine di valutazione

  • Cosa succede con l'operatore or?
  • L'idea è la stessa: se il primo valore che leggiamo è già True, non c'è bisogno di continuare la valutazione

4. Ordine di Valutazione 4

Il tuo turno!

  • Prova ad indovinare il risultato delle espressioni sulla destra
  • Inserisci la tua risposta nella variabile risp
  • Infine esegui il codice e verifica il tuo punteggio

5. Errori 1

Errori nella valutazione

  • Che succede se un'espressione booleana contiene del codice che genererebbe un errore?
  • Il programma dovrebbe terminare? Non sempre!
  • Proviamo a generare di proposito un errore
  • Lanciato il codice?
  • Nota che 'dopo' non viene stampato perchè il programma si interrompe prima
  • Facciamo un'altra prova...
  • Cosa ti aspetti che succeda in questo caso?
  • Verifica eseguendo il codice!
  • Perché Python ha prodotto un risultato senza lamentarsi?

5. Errori 2

Il tuo turno!

  • Guarda le espressioni seguenti, e per ciascuna cerca di indovinare quale risultato produce, o se dà errore

5. Errori 3

Il tuo turno!

6. Comparazione 1

Operatori di comparazione

Comparatore Descrizione
a == b True se e solo se a = b
a != b True se e solo se a ≠ b
a < b True se e solo se a < b
a > b True se e solo se a > b
a <= b True se e solo se a ≤ b
a >= b True se e solo se a ≥ b

Con gli operatori di comparazione puoi costruire espressioni che ritornano un valore booleano

6. Comparazione 2

Qualche esempio

  • 3 == 5 -> False
  • 3 != 5 -> True
  • 3 != 3 -> False
  • a,b = 3,5
  • a == a -> True
  • a == b -> False
  • a == b-2 -> True
  • 3 < 5 -> True
  • 5 < 5 -> False
  • 5 <= 5 -> True

6. Comparazione 3

Le comparazioni sono espressioni che producono booleani

⮕ possiamo assegnare il risultato ad una variabile

7. Congiungere Operazioni 1

Congiungere operazioni

Dato un paio di quantità x, y = 7, 5

Trova una espressione booleana che ci dice se x e y sono entrambe maggiori di zero

Attenzione! La scrittura x and y > 0 NON è corretta

Perché?

Apparentemente su alcuni input sembra funzionare...

Ma funziona proprio su tutti?

Qualcosa non va...

Python ha implicitamente considerato l'espressione come se fosse con queste parentesi

(x) and (y > 0)

Quindi Python sta rilevando il valore logico dell'intero -3, che essendo diverso da 0 viene considerato True

Se invece provassimo a mettere noi le parentesi: (x and y) > 0?

Ancora non funziona... prova a pensare bene a tutti i passi che Python farà per calcolare l'espressione

Vai avanti per la soluzione!

7. Congiungere Operazioni 2

Perché (x and y) > 0 non funziona

Sia x che y vengono considerate singole espressioni booleane, quindi Python internamente ridurrà l'espressione nei seguenti passi:

  1. (True and True) > 0
  2. True > 0
  3. 1 > 0
  4. True

Quindi qual è la soluzione corretta? x > 0 and y > 0

7. Congiungere Operazioni 3

Il tuo turno!

  • Prova ad indovinare il risultato delle espressioni in basso (o se producono errori)

7. Congiungere Operazioni 4

8. Esercizi 1

Il dottor Angelo possiede un prato di area quadrata di lato d=100 metri che viene accudito ogni settimana da Jobe il giardiniere. Jobe passa sempre meticolosomente il tagliarbe su tutta l’area del prato, ma un giorno il dottore decide di rendere più elaborato il giardino e chiede a Jobe di tagliare solo alcune zone. Purtroppo, Jobe non è molto forte in geometria e per agevolarlo il dottore inventa un sensore in grado di rilevare la posizione, collegato ad una spia che si illumina solo quando il tagliaerbe va azionato.

Scrivi un’espressione che date due coordinate x,y, produca True quando il tagliaerbe è nella zona verde chiaro, e False altrimenti.

  • Nota che l'origine delle coordinate è in basso a sinistra
  • NON usare istruzioni if
  • SCRIVI una formula generica usando d (quindi non scrivere 50...)
Image of the exercise

Inserisci la tua espressione, usando x, y e d

Esercizio
Il tagliaerbe 1

8. Esercizi 2

Esercizio - Il tagliaerbe 2

Il dottor Angelo adesso richiede a Jobe di tagliare più zone…

  • NON usare istruzioni if
Image of the exercise

Inserisci la tua espressione, usando x, y e d.

8. Esercizi 3

Esercizio - Il tagliaerbe 3

Il dottor Angelo si è stufato di giardini squadrati, e vuole dividere il prato in diagonale.

  • NON usare istruzioni if
Image of the exercise

Inserisci la tua espressione, usando x e y

8. Esercizi 4

Esercizio - Il tagliaerbe 4

Altro giorno, altra diagonale per Jobe...

  • NON usare istruzioni if
  • SUGGERIMENTO: se non ricordi l'equazione della retta è il momento di cercarla :-)
Image of the exercise

Inserisci la tua espressione, usando x, y e d

8. Esercizi 5

Durante i tuoi studi scopri una mappa di un antico tempio, ove sono custoditi mirabolanti tesori. Il tempio misura d=80 metri di lato ed è un labirinto di corridoi. Sai per certo che alcune aree mostrate in rosso contengono pavimento fragile sotto il quale scorrono fiumi di lava incandescente: per avvertirti del pericolo mentre cammini, ti costruisci un detector che emetterà un suono quando sarai in zone rosse.

Scrivi un’espressione booleana che restituisca True se sei in una zona di pericolo, False altrimenti.

  • NON usare istruzioni if
Image of the exercise

Inserisci la tua espressione, usando x, y e d

Esercizio
Il Tempio di Lava

8. Esercizi 6

Esercizio - Il Salto del Tubo

Un idraulico italiano vede 3 tubi di altezza rispettivamente t1, t2, t3, sopra cui vi sono rispettivamente sono 10, 20, 30 monete. Esaltato, spicca un balzo di altezza h.

Scrivi del codice che stampa quante monete raccoglie (10, 20 o 30).

  • NON usare istruzioni if
  • SUGGERIMENTO: se non sai come fare, riguardati le slide sull'Ordine di valutazione e prova a pensare come produrre dei numeri solo quando una certa condizione è vera...
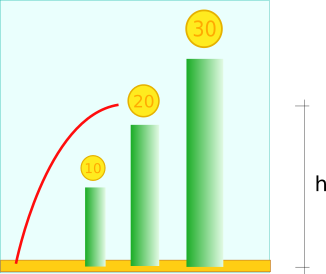
Image of the exercise

Inserisci la tua espressione, usando h, t1, t2, t3

8. Esercizi 7

La lancetta dell’orologio sulla prima Torre di Gradius ha compiuto finora una rotazione di n gradi. Scrivi del codice che mostra True se la lancetta si trova nelle zone evidenziate, False altrimenti.

  • NON usare istruzioni if
  • n può essere maggiore di 360

Ci sono due modi di risolvere il problema:

  1. semplice: potresti scrivere una espressione lunga con diversi and e or
  2. più difficile: riesci a scrivere una sola espressione breve senza and né or?
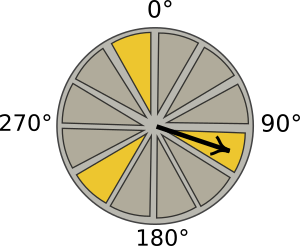
Image of the exercise

Inserisci la tua espressione, usando n.

Esercizio
La Torre di Gradius I

8. Esercizi 8

Esercizio - La Torre di Gradius II

Le lancette dell’orologio sulla seconda Torre di Gradius hanno compiuto finora una rotazione rispettivamente di n e m gradi.

Scrivi del codice che mostri True se entrambe le lancette si trovano nella stessa zona tra quelle evidenziate, False altrimenti.

  • NON usare istruzioni if
  • n e m possono essere maggiori di 360
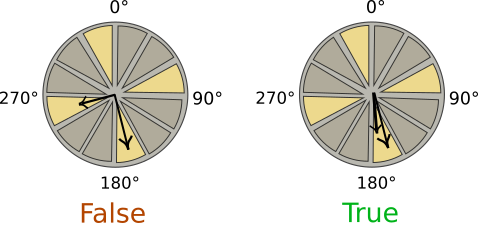
Image of the exercise

Inserisci la tua soluzione, usando n e m